
dS Wiki

|
dS Wiki
|
Method of imagesMethod of images (or method of mirror images) is used in electrostatics (magnetostatics) to simply calculate or visualize the distribution of the electric (magnetic) field of a charge (magnet) in a vicinity to the conducting (superconducting) surface. It is based on the fact that the tangential (normal) component of the electrical (magnetic) field to the surface of a conductor (superconductor) is zero, and that some field E with rot E = 0 and div E = 0 in some region is uniquely defined by its normal component over the surface which confines this region (the uniqueness theorem). |
|
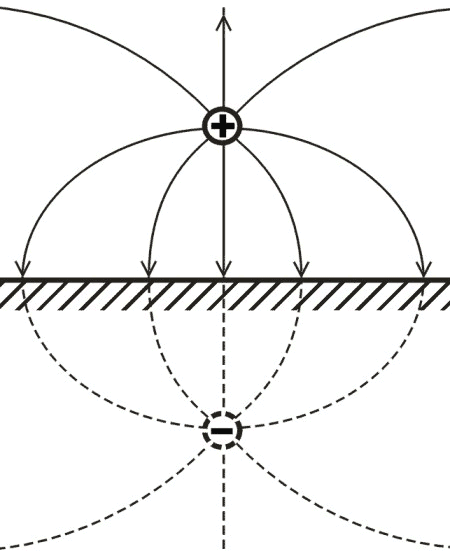
Fig. 1. The field of a charge near a flat conducting surface, found by the method of images. |
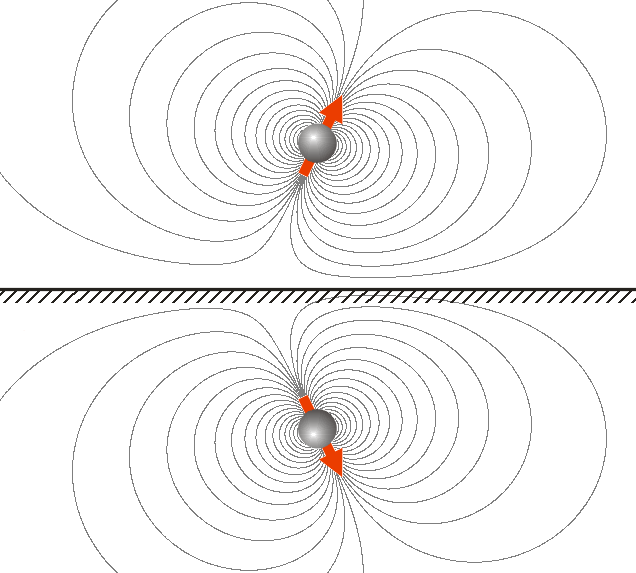
Fig. 2. A magnetic dipole over the superconducting surface. The field between the magnet and surface is the same as between this magnet and a symmetric one. |
|
A textbook example [1] is an infinitely flat conducting surface (see Fig. 1). In this case the field
distribution between the surface and a charge (right side in Fig. 1) is the same as between this
charge and another charge (imaginary charge), which is the mirror image of the real charge in
respect to the surface but has the opposite sign. Evidently, in case of an electrical dipole,
the vector of the mirrored dipole will have the opposite sign. Therefore, the force between the
electrical charge or system of charges and the conducting surface is attractive.
In case of magnet-superconductor pair (the superconductor here is ideal, to which the magnetic field does not penetrate), the mirror image of the magnet will have a magnetization vector which is mirrored but of the same sign (Fig. 2). This can be thought as due to additional sign change upon mirroring of an axial vector which the magnetization is. The force between the magnet and the superconducting surface is therefore repulsive. |
|
|
Method of frozen mirror images is a modification of the method of images for magnet-superconductor systems that has been introduced [2] to take into account the magnetic flux pinning phenomenon. The method gives a simple representation of the magnetic field distribution generated by a magnet (a system of magnets) outside an infinitely flat surface of a perfectly hard (with infinite pinning force) type-II superconductor in a most general field cooled (FC) case, i.e. when the superconductor goes into superconducting state been already exposed to the magnetic field.
The name originates from the replacement of certain elements in the original layout with imaginary magnets, which replicates the boundary conditions of the problem (see Dirichlet boundary conditions). In a simplest case of the magnetic dipole over the flat superconducting surface (see Fig. 3), the magnetic field, generated by a dipole moved from its initial position (at which the superconductor is cooled to the superconducting state) to a final position and by the screening currents at the superconducting surface, is equivalent to the field of three magnetic dipoles: the original one (1), its mirror image (3), and the magnetization inversed mirror image of it in its initial position (2). The method has been shown to work for the melt-textured high temperature superconductors (MT HTSC) [2], which are characterized by a strong pinning and is useful for calculation of the interaction in magnet-HTSC systems such as superconducting magnetic bearings [3], superconducting flywheels [4], MAGLEV [3], etc. [5,6] |
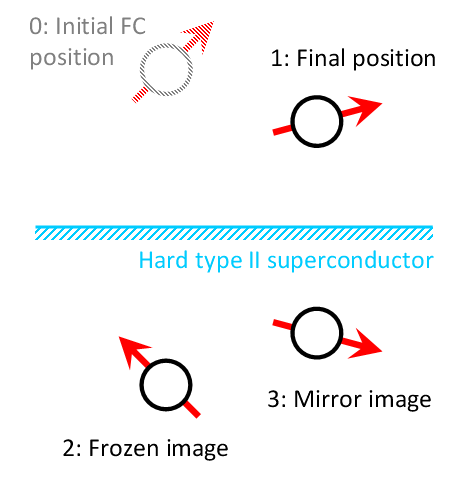
Fig. 3. Illustration of the frozen mirror image method for a simplest case of the magnetic dipole over a flat superconducting surface. |
References
|
|
© kord 2004